GiuliaP
Riguardo la curtosi non sono così convinta di quello che dici. Questo per non parlare del survivorship bias anche nella stima del rischio, quando si fanno distinzioni
tra indici, titoli ed altro.
Se ti riferisci alla sovrastima del rischio, non dovrebbe essere il contrario? O forse non ho capito il tuo discorso?
Imar
Questa è una osservazione molto interessante (dal che capisco che non ti occupi di MIBO ....ma più probabilmente di STE50 o S&P500).. con interessanti ripercussioni
anche in termini di pricing
Cren
Per chiarezza, Thymon: ho capito male quando affermo di aver compreso quanto segue?
«Su determinati indici è presente un effetto di ritorno verso la media che rende la quantificazione del rischio mediante "square root rule" un processo tendente a
sovrastimare i rischi piuttosto che a sottostimarli».
Ma tu ti riferisci a livelli dell'indice, rendimenti dell'indice, livelli della IV, livelli della RV... o cosa?
Rileggendo la mia frase e i vostri commenti direi che la mia "estrema sintesi" era sicuramente troppo estrema.
Provo ad elaborare meglio. La questione è se sia corretto utilizzare la relazione Vola-sqr(t) per traslare nel tempo la nostra stima di Vola (senza quindi introdurre
ulteriori errori alla stima). La matematica ci dice che tale relazione è valida se sono rispettate certe condizioni e alcuni studi empirici possono dirci se nei
mercati di nostro interesse quelle condizioni esistono o meno. Come accennato, lo studio a cui mi riferivo è stato fatto sul mercato equity US e su due indici
(Nasdaq100 e SP500). La mia interpretazione dei risultati è che tale relazione sia valida sia su single stock sia su index e che quindi possa essere utilizzata nel "modello"
di stima del rischio senza produrre distorsioni apprezzabili.
Nel caso di Index, l'utilizzo di tale relazione, sembra portare ad una sovrastima della vola (suppongo proporzionale al numero dei costituenti) ma per gli obiettivi della
discussione basta dire che la "relazione" è ancora valida.
Ad ogni modo, allego un estratto (stavolta sono tre pagine
Non ho invece evidenza se anche la Vola della Vola rispetta tali condizioni e spero che l'introduzione di VVix stimoli la ricerca in tal senso.
GiuliaP
Una stima efficace per la CH, per noi è sempre e comunque un limite inferiore invalicabile. Ed a prescindere dal nostro calcolo del rischio, per quanto complesso,
dovremo comunque aggiungere un certo errore di tolleranza.
Sulla singola giornata, non c'è dubbio che stimare un rischio inferiore a quello che dice CH risulta completamente inutile. Essendo però lo SOA costante attraverso
la Moneyness ( VeryDOTM e OTM potrebbero avere lo stesso valore) mi pare una semplificazione eccessiva quando dovessimo traslare questo valore nel tempo.
Rimane da vedere se troviamo una alternativa migliore per quantificare gli eventi "abbastanza estremi".
Imar
Su questo mi permetto di non essere troppo d'accordo.
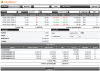
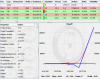
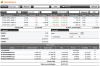
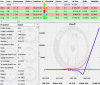
Riporto in allegato una tabella molto interessante; sono i put sull'S&P 500 10 gg prima del crollo del 1987 (per sentire il "peso" di quei numeri, moltiplicate per 500
ed avrete il valore di un singolo miserrimo lotto, riferito all'S&P "big").
Per quanto riguarda gli eventi estremi, non sono sicuro che un eventuale stima del rischio debba includerli, o meglio dipende molto da come utilizzeremo tale stima
del rischio di portafoglio, quali decisioni baseremo su tale stima e quindi quali effetti produrrebbe sul portafoglio stesso. (Discorso un po' lungo, ma a scanso di
equivoci, non sto dicendo che non siano eventi da tenere in qualche modo in considerazione).
Buona Pasqua a tutti e grazie a voi per l'interessante discussione che sta venendo fuori.
Thymon