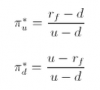Stai usando un browser molto obsoleto. Puoi incorrere in problemi di visualizzazione di questo e altri siti oltre che in problemi di sicurezza. .
Dovresti aggiornarlo oppure usarne uno alternativo, moderno e sicuro.
Dovresti aggiornarlo oppure usarne uno alternativo, moderno e sicuro.
Charles M. Cottle
- Creatore Discussione tucciotrader
- Data di Inizio
tucciotrader
Trader Calabrese
Quindi è 0,50 non c'è altra risposta...
Cren
Forumer storico
In un mercato senza opportunità di arbitraggio sì.Quindi è 0,50...
A questo punto sarebbe indebitamente divertente se tu riportassi la risposta nel posto dove hai chiesto lumi senza granchè di spiegazioni a corredo

Ultima modifica:
tucciotrader
Trader Calabrese
In un mercato senza opportunità di arbitraggio sì.
Io avevo capito che la soluzione era che il dato della distribuzione futura non è necessario, ma basta applicare il metodo binomale (uno step), quindi probabilità risk neutral.
...
EDIT: e allora potrei azzardare anche una vola implicità del 15,80% annualizzata
Intendo 1% giornaliera: 60% di fare +1% e 40% di fare -1%
Ultima modifica:
Cren
Forumer storico
Se il mercato è privo di opportunità di arbitraggio, ovvero assumendo che quel 60% di probabilità sconti un premio per il rischio positivo, solo una misura di probabilità neutrale al rischio puoi usare.Io avevo capito che la soluzione era che il dato della distribuzione futura non è necessario, ma basta applicare il metodo binomale (uno step), quindi probabilità risk neutral.
Quindi, con tasso privo di rischio nullo, hai 50% di probabilità di salire o scendere dello stesso ammontare percentuale (volatilità) e quindi il valore della Call non può che essere il 50% del payoff.
tucciotrader
Trader Calabrese
Quindi, con tasso privo di rischio nullo, hai 50% di probabilità di salire o scendere dello stesso ammontare percentuale (volatilità) e quindi il valore della Call non può che essere il 50% del payoff.
Spesso per semplicità si suppone tasso privo di rischio nullo. Come cambia la situazione se applichiamo un tasso privo di rischio NON nullo?
Cren
Forumer storico
Ti basta calcolartelo.Come cambia la situazione se applichiamo un tasso privo di rischio NON nullo?
u e d sono gli incrementi del prezzo tra un istante e il successivo, quindi, se per esempio passi da 100 a 101, u = 101/100 = 1.01.
Allegati
Ultima modifica:
tucciotrader
Trader Calabrese
Quando si parla di 0,6 di andare a 101 e 0,4 di andare a 99 si parla solo del primo step del metodo binomale o delle possibilità del risultato a scadenza?
Dopo che molti si erano incartati su BSM, finalmente è arrivata latanto attesa risposta!

Dopo che molti si erano incartati su BSM, finalmente è arrivata latanto attesa risposta!
Sulla base delle informazioni date puoi calcolare un prezzo teorico con un banalissimo modello binomiale.
Ma prima di dare una qualsiasi risposta bisogna chiedere la natura di quelle probabilità (sono naturali o sintetiche?). Con un minimo di ragionamento, comunque, è possibile vedere come in questo particolarissimo caso (tasso riskless pari a 0%) le due probabilità coincidano.
Quindi, conosci i possibili payoff nei due stati considerati (prezzo a 101 e prezzo a 99), conosci le probabilità sintetiche (che coincidono con le reali) ed il tasso a cui scontare.
Il prezzo teorico è il valore attuale del payoff atteso.
Tutto questo ti permette di calcolare un prezzo solo teorico. In pratica è un esercizio da universitario, nulla di concreto. Il prezzo vero sarà un altro.

skew
Nuovo forumer
Se dici così, non puoi essere d'accordo che il valore dell'opzione è 0.5.... dovresti pensare che viene scambiata a 0.6 (dato che è implicito il "no free lunch" principle).
IMHO, il trabocchetto della domanda sta proprio nel fatto che ti danno un dato (la distribuzione effettiva futura) che non è necessario per valutare le opzioni (e meno male, sennò sarebbe impossibile, dato che nessuno la conosce ex ante).
Qua occorre l'interpretazione autentica di Skew, mandagli un messaggio di passare di qua.
Ovviamente il trabocchetto è proprio lì!
Hai la distribuzione futura con esattezza... ma ai fini del pricing te ne fai ben poco
Similar threads
Users who are viewing this thread
Total: 1 (members: 0, guests: 1)