Per quanto riguarda il Capm e l'analisi dei residui, la prof. ha fatto in questo modo;
x = c(7, 9, 6, 14, 8, 12, 10, 4, 2, 11, 1, 8) #
y = c(26, 20, 28, 16, 23, 18, 24, 26, 38, 22, 32, 25) #
X = cbind(1,x) # Matrice x
n = nrow(X) # Numero osservazioni
p = ncol(X) # Numero coef. da stimare
XtXinv = solve( t(X) %*% X ) # Matrice (X>X)−1
b = XtXinv %*% t(X) %*% y # Stime coef. regressione ˆ
yfit = X %*% b # Valori Stimati ˆy
e = y - yfit # Residui
s2 = sum(e^2)/(n-p) # Stima di 2
s2*XtXinv # Matrice Var(ˆ) = ˆ2(X>X)−1
sqrt(diag(s2*XtXinv)) # Errore std stime dei coefficienti
R2 = 1 - sum(e^2)/sum((y-mean(y))^2) # Coef. di determinazione R2
0.8252894
mod = lm(y ~ x) # Modello di regressione semplice
summary(mod)
Invece per quanto riguarda il modello sopra fatto da te, i numeri nel par cosa significano ? devo riportarli anche io ?
La tua prof.ssa ti ha giustamente messo per esteso tutto il procedimento di regressione in forma matriciale così come lo troveresti su qualsiasi testo di econometria.
Alla fine ti ha messo anche la stessa funzione che ho usato io, cioè
lm(), probabilmente per farvi vedere che i risultati erano identici.
Io ho fatto la stessa cosa dentro al ciclo
for() per ciascuna coppia titolo ~ indice e ne ho estratto le statistiche di interesse.
Come ti ho già detto,
par() sono solo impostazioni grafiche che puoi anche non riportare ma che servono per rappresentare i dati come vuoi tu.
In particolare,
par(mfrow = c(a,b))
divide la schermata di
plot in
a righe e
b colonne, come ho fatto io.
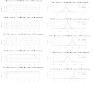
dove si vede che i residui sopra hanno una struttura di autocorrelazione debole
Scusa, ma prima di mettervi a fare questo esercizio qualche straccio di rudimento di base di econometria ve l'avranno pur dato, no?
Nell'immagine che ho allegato prima, cioè questa
la colonna di correlogrammi di sinistra rappresenta il coefficiente di autocorrelazione parziale in funzione di diversi periodi di ritardo (è una procedura di base di analisi delle serie storiche che è praticamente
standard): se il modello CAPM descrivesse perfettamente la realtà che vuole rappresentare, l'autocorrelazione dei residui (cioè tutto ciò che non è spiegato dal modello) sarebbe molto debole, diciamo statisticamente non significativa entro un certo intervallo di confidenza (solitamente 95%).
Le righine nere verticali sono le autocorrelazioni a diversi ritardi e le righine blu orizzontali sono gli intervalli fiduciari: vedi che le righine nere verticali "tagliano" le righine blu orizzontali mediamente "poco" e quindi non oltrepassano l'intervallo fiduciario?
Una curiosità, quale di queste:
- c'era il corso di econometria ma non l'hai seguito prima di fare il laboratorio;
- c'era il corso di econometria ma l'hai seguito poco e male perché eri distratto dai pantaloni a vita inguinale della tua vicina di posto;
- la prof.ssa vi ha spiegato queste cose ma non segui il laboratorio e ti fai passare gli appunti;
- il comando "?" su R non ti funziona;
- non hai nessuna voglia di leggere il codice e capire riga per riga come funziona né di guardare la tonnellata di esempi delle pagine di aiuto di R.
La mia impressione è che se ti presenti all'esame orale con i dubbi che hai ora, quella ti fa a pezzi.