Mercuzio
ex Drenaggio
Salve a tutti,
In conseguenza a diverse richieste giuntemi a riguardo di argomenti matematici-statistici, apro questo 3d dedicato alla risoluzione degli stessi..
In seguito vedremo se e come ampliare questo 3d con la didattica.
Per adesso inizio con un quesito giuntomi per MP:
"Come determinare il coefficiente di correlazione di Pearson" tra due variabili aleatorie o statistiche?"
Una breve definizione di questo coefficente:
Il coefficiente di correlazione (lineare) di Pearson serve a definire il livello di correlazione fra due variabili aleatorie o statistiche, oscillando fra i valori di 1 e -1 determina i seguenti stati:
Lo stato incorrelato (=0) identifica due variabili non correlate fra loro, cioè che si muovono in modi totalmente diversi l'una dall'altra (il che non significa "indipendenti")
Lo stato inversamente correlato (<0) identifica due variabili che si muovono sempre in modo contrario, cioè quando una cresce l'altra decresce.
Il coefficiente di correlazione (lineare) di Pearson è infine dato dalla formula:
 . cioè: coeff.= covarianza(xy)/(St.Dev(x)*St.Dev(y))
. cioè: coeff.= covarianza(xy)/(St.Dev(x)*St.Dev(y))
dove x e y sono le due variabili
Ed ora la formula per PRT:
////////////////////////////////////////////////////////////////////////////////
REM: Parametri da creare: period=?
x=?
y=?
REM Covarianza
xav=average[period](x)
yav=average[period](y)
scartox=x-xav
scartoy=y-yav
pscarti=scartox*scartoy
covarianza=average[period](pscarti)
REM Calcolo Standard Deviation senza passare dalla funzione standard
MMx=average[period](x)
ax=(square(x-MMx))
sx=summation[period](ax)
StDevx=SQRT(sx/(period-1))
MMy=average[period](y)
ay=(square(y-MMy))
sy=summation[period](ay)
StDevy=SQRT(sy/(period-1))
REM Calcolo il coeff di Pearson
Pcoeff=covarianza/(StDevx*StDevy)
return Pcoeff as "Pcoeff", 0 as "0"
////////////////////////////////////////////////////////////////////////////////
Naturalmente parliamo di misure campionarie e pertanto è necessario decidere l'ampiezza del campione tramite il parametro "period" da creare in PRT....le variabili "X" e "Y" sono chiaramente sconosciute in questa formula e possono essere sostituite con ciò che si vuole.
Sfortunatamente PRT non consente di utilizzare flussi di dati provenienti da titoli diversi nella stessa formula, e pertanto i flussi in questione dovranno necessariamente derivare dallo stesso titolo (es. due differenti medie mobili del solito prezzo)...
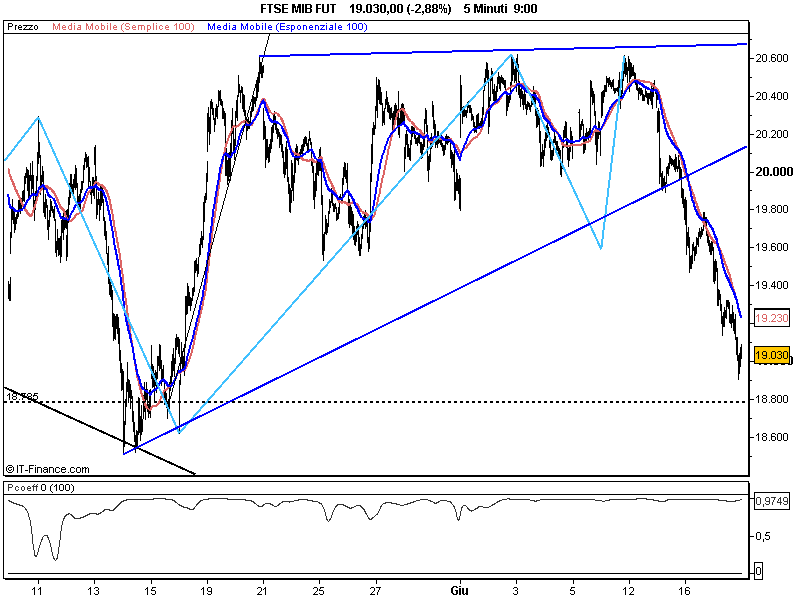
Ad esempio qui sotto potremmo fare il caso di due medie a 100 periodi, di cui la prima di tipo aritmetico (rossa) e la seconda esponenziale (blu)...quale sarà il loro livello di correlazione..?
E vediamo che in pratica sono sempre correlate (nel campione da nuoi considerato), cioè i loro valori non toccano mai lo zero, ne tantomeno scendono sotto zero....quindi ci sono solo casi in cui abbiamo + o - correlazione...
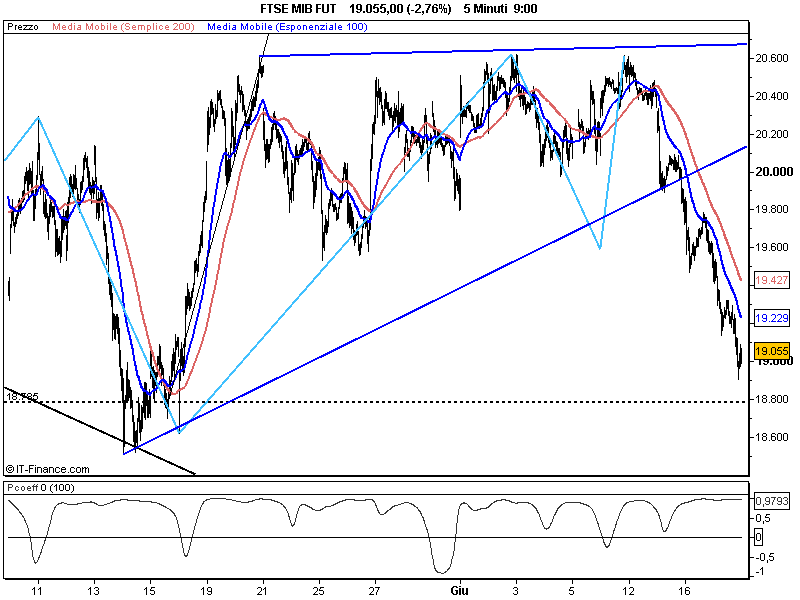
Se invece modifichiamo la prima media aritmetica portandola a 200 periodi contro i 100 di prima.....
Vediamo che affiorano anche casi di non correlazione e correlazione inversa...
saluti.
In conseguenza a diverse richieste giuntemi a riguardo di argomenti matematici-statistici, apro questo 3d dedicato alla risoluzione degli stessi..
In seguito vedremo se e come ampliare questo 3d con la didattica.
Per adesso inizio con un quesito giuntomi per MP:
"Come determinare il coefficiente di correlazione di Pearson" tra due variabili aleatorie o statistiche?"
Una breve definizione di questo coefficente:
Il coefficiente di correlazione (lineare) di Pearson serve a definire il livello di correlazione fra due variabili aleatorie o statistiche, oscillando fra i valori di 1 e -1 determina i seguenti stati:
-
, le variabili x e y si dicono direttamente correlate, oppure correlate positivamente;

, le variabili x e y si dicono incorrelate;
, le variabili x e y si dicono inversamente correlate, oppure correlate negativamente.
Lo stato incorrelato (=0) identifica due variabili non correlate fra loro, cioè che si muovono in modi totalmente diversi l'una dall'altra (il che non significa "indipendenti")
Lo stato inversamente correlato (<0) identifica due variabili che si muovono sempre in modo contrario, cioè quando una cresce l'altra decresce.
Il coefficiente di correlazione (lineare) di Pearson è infine dato dalla formula:

dove x e y sono le due variabili
Ed ora la formula per PRT:
////////////////////////////////////////////////////////////////////////////////
REM: Parametri da creare: period=?
x=?
y=?
REM Covarianza
xav=average[period](x)
yav=average[period](y)
scartox=x-xav
scartoy=y-yav
pscarti=scartox*scartoy
covarianza=average[period](pscarti)
REM Calcolo Standard Deviation senza passare dalla funzione standard
MMx=average[period](x)
ax=(square(x-MMx))
sx=summation[period](ax)
StDevx=SQRT(sx/(period-1))
MMy=average[period](y)
ay=(square(y-MMy))
sy=summation[period](ay)
StDevy=SQRT(sy/(period-1))
REM Calcolo il coeff di Pearson
Pcoeff=covarianza/(StDevx*StDevy)
return Pcoeff as "Pcoeff", 0 as "0"
////////////////////////////////////////////////////////////////////////////////
Naturalmente parliamo di misure campionarie e pertanto è necessario decidere l'ampiezza del campione tramite il parametro "period" da creare in PRT....le variabili "X" e "Y" sono chiaramente sconosciute in questa formula e possono essere sostituite con ciò che si vuole.
Sfortunatamente PRT non consente di utilizzare flussi di dati provenienti da titoli diversi nella stessa formula, e pertanto i flussi in questione dovranno necessariamente derivare dallo stesso titolo (es. due differenti medie mobili del solito prezzo)...
Ad esempio qui sotto potremmo fare il caso di due medie a 100 periodi, di cui la prima di tipo aritmetico (rossa) e la seconda esponenziale (blu)...quale sarà il loro livello di correlazione..?
E vediamo che in pratica sono sempre correlate (nel campione da nuoi considerato), cioè i loro valori non toccano mai lo zero, ne tantomeno scendono sotto zero....quindi ci sono solo casi in cui abbiamo + o - correlazione...
Se invece modifichiamo la prima media aritmetica portandola a 200 periodi contro i 100 di prima.....
Vediamo che affiorano anche casi di non correlazione e correlazione inversa...
saluti.


