Calcolo rendimenti e Fogli elettronici Calcolo Rendimenti con Foglio di Excel

[GiveMeLeverage]

Ok, grazie mille GiveMe. Così ho fatto un altro piccolo passo avanti.
Non ho capito il discorso sulla costruzione della curva dei forward...
Non è per fare i sofisticati, ma intanto ad imparare non fa mai male, e poi se riusciamo a creare dei modelli di valutazione/analisi dei bond sempre più accurati è tutto a nostro vantaggio.

Gli inflation swap esprimono l'attesa dell'inflazione media per i prossimi x anni.
Se p.e. lo ZC inflation swap 15Y è dell'1,855% (dato al 27.09), ciò significa che il mercato per i prossimi 15 anni si attende un'inflazione media dell'1,855%.
Ma se volessimo sapere quant'è l'attesa dell'inflazione per il 2013 o il 2020 (non fino al, ma per l'anno)?
Poco probabile che coincida con la nostra media...
Invece del tasso spot ci servirebbe il tasso forward (cioè il tasso, calcolato oggi, che parte tra un tempo x e dura y).
Avendo a disposizione la serie dei tassi spot, possiamo calcolarci i forward grazie alla seguente relazione (nella quale si esprime il fatto che un capitale impiegato per un tempo t02 dovrà essere uguale allo stesso capitale impiegato per un tempo t01 e poi per un tempo t12, con t02 = t01 + t12):

(1+r02)^t02 = (1+r01)^t01 * (1+r12)^t12

r01 = primo tasso spot
r02 = secondo tasso spot
r12 = tasso forward

t0 = oggi
t1 = data finale del primo spot = data iniziale del forward
t2 = data finale del secondo spot = data finale del forward

t01 = t1- t0 = durata del primo spot
t02 = t2- t0 = durata del secondo spot
t12 = t2- t1 = t02 - t01 = durata del forward


Da cui si ricava l'equazione esplicita del forward:

r12 = ((1+r02)^t02 / (1+r01)^t01))^(1/t12) - 1


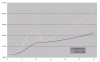
Allego un grafico per mostrare la differenza tra tassi spot (= inflazione media da oggi all'anno x) e tassi forward durata 1 anno (= inflazione media nell'anno x).

 

[sesp]

Gli inflation swap esprimono l'attesa dell'inflazione media per i prossimi x anni.
Se p.e. lo ZC inflation swap 15Y è dell'1,855% (dato al 27.09), ciò significa che il mercato per i prossimi 15 anni si attende un'inflazione media dell'1,855%.
Ma se volessimo sapere quant'è l'attesa dell'inflazione per il 2013 o il 2020 (non fino al, ma per l'anno)?
Poco probabile che coincida con la nostra media...

FANTASTICO GiveMe!!!!
Grazie infinite per questa spiegazione e soprattutto per la pazienza.
Provo subito ad applicarlo al modello che sto costruendo.

Hai per caso visto i files che ho allegato ieri?
Mi farebbe piacere ricevere commenti e suggerimenti: se riusciamo a costruire un modello decente poi ne beneficiamo tutti.

 

[sesp]

Ho provato ad inserire i tassi FWD a 1 anno dell'inflazione nel foglio test allegato ieri.
Ammesso che i calcoli dei FWD siano corretti (chiedo gentilmente verifica a chi è avvezzo a questi calcoli per me molto complicati... ) il rendimento si discosta di poco da quello calcolato brutalmente con i soli ZC Swap.
Cio che cambia sensibilmente è invece la cedola media.

Ora, non so se ho seguito una moetodologia corretta, per cui vi chiedo lumi in merito.
Allego immagine dei nuovi calcoli per confronto.

 

[GiveMeLeverage]

Ho provato ad inserire i tassi FWD a 1 anno dell'inflazione nel foglio test allegato ieri.
Ammesso che i calcoli dei FWD siano corretti (chiedo gentilmente verifica a chi è avvezzo a questi calcoli per me molto complicati... ) il rendimento si discosta di poco da quello calcolato brutalmente con i soli ZC Swap.
Cio che cambia sensibilmente è invece la cedola media.

Ora, non so se ho seguito una moetodologia corretta, per cui vi chiedo lumi in merito.
Allego immagine dei nuovi calcoli per confronto.

Ad occhio e croce mi sembra corretto.
La differenza tra i due metodi (ZC Swap diretto e forward) è di ca. 5 pb sia sulla cedola media che sul rendimento, o sbaglio?

Visto il risultato quasi identico, direi che all'atto pratico si può utilizzare l'inflazione media, almeno fino a quando la curva rimane così piatta e regolare.

 

[sesp]

Ad occhio e croce mi sembra corretto.
La differenza tra i due metodi (ZC Swap diretto e forward) è di ca. 5 pb sia sulla cedola media che sul rendimento, o sbaglio?

Visto il risultato quasi identico, direi che all'atto pratico si può utilizzare l'inflazione media, almeno fino a quando la curva rimane così piatta e regolare.

Sì, esatto. Abbiamo uno scarto di 5 basis point sia su cedola sia su rendimento.
Ok, al mometo i due metodi sono praticamente equivalenti, ma come dici tu potremmo avere differenze evidenti in caso di curva "nervosetta"....
Per cui, senza saper nè leggere nè scrivere, per quel che costa metto sui fogli sia la stima con ZC Inflat sia con FWD Inflat, così se la curva impazzisce vediamo cosa succede e quant'è la differenza.
Grazie mille per aver dato una controllata al mio lavoro e grazie ancora per l'aiuto.

 

[arckan]

Buongiorno, allego il foglio di Maino per i BTP€I aggiornato (ho inserito i pulsanti cancella e stampa e qualche altro restyling).
Spero possa essere utile.

NB: se si seguono con attenzione le note alle varie caselle è preciso al centesimo

 

[Fas]

calcolo rendimenti ZC con aliquota mista

buongiorno a tutti,
gentilmente chiedo a qualcuno di voi se ha mai affrontato il problema di come calcolare il rend netto di uno ZC con il sistema di aliquota doppia che sta per entrare in uso.
grazie mille

 

[lamax]

Buonasera a tutti, volevo sapere se è possibile con il foglio di Maino riuscire a calcolare la ritenuta sulla cedola al 12.5% fino al 31/12 e poi passare alla nuova tassazione, cioè 20%.
Grazie

 

[gorion83]

Buongiorno, allego il foglio di Maino per i BTP€I aggiornato (ho inserito i pulsanti cancella e stampa e qualche altro restyling).
Spero possa essere utile.

NB: se si seguono con attenzione le note alle varie caselle è preciso al centesimo

Complimenti. funziona anche per gli OAT€i e i Bund€i vero?

Complimenti anche a GiveMeLeverage e a Sesp per l'ottimo lavoro sulla stima per le inflation linked

 

[chicco]

Buonasera a tutti, volevo sapere se è possibile con il foglio di Maino riuscire a calcolare la ritenuta sulla cedola al 12.5% fino al 31/12 e poi passare alla nuova tassazione, cioè 20%.
Grazie

Credo che bisogno farlo manualmente, individuano tutte le celle che dipendono da quella del 12,5%; non è possibile, come detto da qualcuno, inserire semplicemente il 20% al posto del 12,5%.....questo sballerebbe tutto