Imprimatur 1632 ( pubblicazione )
« Questo modo di filosofare tende alla sovversion di tutta la filosofia naturale, ed al disordinare e mettere in conquasso il cielo e la Terra e tutto l'universo. »
(Simplicio nel Dialogo sopra i due massimi sistemi del mondo, Giornata prima)
Il Dialogo sopra i due massimi sistemi del mondo è un'opera di trattatistica scientifica composta da Galileo Galilei negli anni tra il 1624 il 1630, per poi ricevere l'imprimatur nel 1632, anno della sua prima pubblicazione. E’ scritta sotto la forma di dialogo.
Riflessione serale ...
In questo post riporto un breve spezzone di questo trattato , dove Galileo spiega come calcolare la velocità di caduta tenendo in considerazione il fattore di accelerazione , e parlando del quadrato dei tempi.
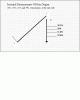
In un movimento al ribasso succede la stessa cosa , in un’ oscillazione ciclica la massima magnitudine ( detta alla Hurst  ) corrispondente al punto dove il mercato inverte , c'è da dire che dapprima può presentare una fase di distribuzione più o meno lunga , ma questo al momento esula dal discorso.
) corrispondente al punto dove il mercato inverte , c'è da dire che dapprima può presentare una fase di distribuzione più o meno lunga , ma questo al momento esula dal discorso.
Il tempo della discesa può essere stimato in termini di periodo tramite il bilanciamento del TEMPO come Gann sappiamo sostiene , ma se l’oscillazione ciclica formasse un massimo al di là dell' ipotetico baricentro temporale teorico ( e questo è confermato a posteriori ) o meglio detto , fossimo in presenza di un trend rialzista , che avvalla una plausibile discesa e conseguente chiusura del ciclo in essere in minor tempo rispetto alla salita potremmo dire anche che :
Questo può corrispondere ad una frazione del bilanciamento , ad esempio 25% , o 12,5% se il trend rialzista è molto forte.
Gann utilizzava la suddivisione in ottavi del range sia in TEMPO che in PREZZO . ( tale suddivisione è derivata da precisi e determinati angoli astronomici.)
Il bilanciamento e la durata di un ciclo possono anche essere individuati tramite l’identificazione di determinati aspetti planetari coincidenti ai punti di massimo e di minimo , e ad altri eventi citati in post precedenti.
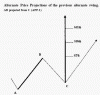
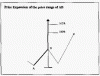
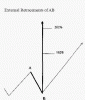
Avendo una stima della durata del movimento di recoil , dopo l’inversione e più precisamente dopo aver misurato la perdita di punti in uno specifico arco temporale sottomultiplo del probabile periodo di tempo necessario a chiudere il ciclo in essere , è possibile valutare quale estensione sia possibile tenendo in considerazione la possibile accelerazione del movimento.
Estensione che può essere comparata con determinati livelli o espansioni di Fibonacci per verificare se sussistono delle sinergie.
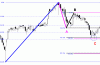
Ovviamente non tutti i cicli culminano con picco profondo , alcuni mentre si apprestano a formare il minimo evidenziano un R.O.C in divergenza "perdita di velocità", ma questo non toglie il fatto di poter misurare un determinato segmento appartenente ad un sottociclo di grado minore che viene investito in pieno dalla forza delle componenti maggiori e dunque evidenzia un’ accelerazione ribassista in costante aumento.
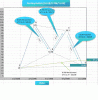
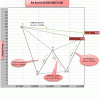
Target estensione = 280 punti pari ad un livello XOP
Coperti 100 in 40’ minuti
Rimanenti = 180
Intensità ciclica superiore = FORTE
Tempo previsto per raggiungimento supporto :
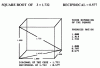
√( 180 * 40 2 ) / 100 = 53 minuti e mezzo .
Totale tempo = 1’ ora e mezza c.a
Da cui controllare se il tempo previsto rientra nei limiti temporali restanti per la chiusura del ciclo in essere.
Ma ora vi lascio a una buona lettura…..
SALV. Avanti di ogni altra cosa, bisogna considerare come il movimento de i gravi descendenti non è uniforme, ma partendosi dalla quiete vanno continuamente accelerandosi; effetto conosciuto ed osservato da tutti, fuor che dal prefato autore moderno, il quale, non parlando di accelerazione, lo fa equabile.
Ma questa general cognizione è di niun profitto, quando non si sappia secondo qualproporzione sia fatto questo accrescimento di velocità, conclusione stata sino a i tempi nostri ignota a tutti i filosofi, e primieramente ritrovata e dimostrata dall'Accademico, nostro comun amico: il quale, in alcuni suoi scritti non ancor pubblicati, ma in confidenza mostrati a me e ad alcuni altri amici suoi, dimostra come l'accelerazione del moto retto de i gravi si fa secondo i numeri impari abunitate, cioè che segnati quali e quanti si voglino tempi eguali, se nel primo tempo, partendosi il mobile dalla quiete, averà passato un tale spazio, come, per esempio, una canna, nel secondo tempo passerà tre canne, nel terzo cinque, nel quarto sette, e cosí conseguentemente secondo i succedenti numeri caffi, che in somma è l'istesso che il dire che gli spazii passati dal mobile, partendosi dalla
quiete, hanno tra di loro proporzione duplicata di quella che hanno i tempi ne' quali tali spazii son misurati, o vogliam dire che gli spazii passati son tra di loro come i quadrati de' tempi.
SAGR. Mirabil cosa sento dire. E di questo dite esserne dimostrazion matematica?
SALV. Matematica purissima, e non solamente di questa, ma di molte altre bellissime passioni attenenti a i moti naturali e a i proietti ancora, tutte ritrovate e dimostrate dall'amico nostro: ed io le ho vedute e studiate tutte con mio grandissimo gusto e meraviglia, vedendo suscitata una nuova cognizione intera, intorno ad un suggetto del quale si sono scritti centinaia di volumi; e né pur una sola dell'infinite conclusioni ammirabili che vi son dentro, è stata osservata e intesa da alcuno prima che dal nostro amico.
SAGR. Voi mi fate fuggir la voglia d'intender piú oltre de i nostri cominciati discorsi, e solosentire alcuna delle dimostrazioni che mi accennate; però, o ditemele al presente, o almeno datemi ferma parola di farne meco una particolare sessione, ed anco presente il signor Simplicio, se avrà gusto di sentire le passioni ed accidenti del primario effetto della natura.
SIMP. Averollo indubitatamente, ancorché, per quanto appartiene al filosofo naturale, io non credo che il descendere a certe minute particolarità sia necessario, bastando una general cognizione della definizion del moto e della distinzione di naturale e violento, equabile e accelerato, e simili; ché quando questo non fusse bastato, io non credo che Aristotile avesse pretermesso di insegnarci tutto quello che fusse mancato.
SALV. Può essere. Ma non perdiamo piú tempo in questo, ch'io prometto spenderci una meza giornata appartatamente per vostra sodisfazione, anzi pur ora mi sovviene avervi un'altra volta promesso di darvi questa medesima sodisfazione.
E tornando al nostro cominciato calcolo del tempo nel quale il grave cadente verrebbe dal concavo della Luna sino al centro della Terra, per proceder non arbitrariamente e a caso, ma con metodo concludentissimo, cercheremo prima di assicurarci, con l'esperienza piú volte replicata, in quanto tempo una palla, verbigrazia, di ferro venga in Terra dall'altezza di cento braccia.
SAGR. Pigliando però una palla di un tal determinato peso, e quella stessa sopra la quale noi vogliamo far il computo del tempo della scesa dalla Luna.
SALV. Questo non importa niente, perché palle di una, di dieci, di cento, di mille libbre, tutte misureranno le medesime cento braccia nell'istesso tempo.
SIMP. Oh questo non cred'io, né meno lo crede Aristotile, che scrive che le velocità de i gravi descendenti hanno tra di loro la medesima proporzione delle loro gravità.
SALV. Come voi, signor Simplicio, volete ammetter cotesto per vero, bisogna che voi crediate ancora, che lasciate nell'istesso momento cader due palle della medesima materia, una di cento libbre e l'altra d'una, dall'altezza di cento braccia, la grande arrivi in Terra prima che la minore sia scesa un sol braccio: ora accomodate, se voi potete, il vostro cervello a imaginarsi di veder la gran palla giunta in Terra quando la piccola sia ancora a men d'un braccio vicina alla sommità della torre.
SAGR. Che questa proposizione sia falsissima, io non ne ho un dubbio al mondo; ma che anco la vostra sia totalmente vera, non ne son ben capace: tuttavia la credo, poiché voi risolutamente l'affermate; il che son sicuro che non fareste quando non ne aveste certa esperienza o ferma dimostrazione.
SALV. Honne l'una e l'altra, e quando tratteremo la materia de i moti separatamente, ve lacomunicherò: intanto, per non avere occasione di piú interrompere il filo, ponghiamo di voler fare il computo sopra una palla di ferro di cento libbre, la quale per replicate esperienze scende dall'altezza di cento braccia in cinque minuti secondi d'ora.
E perché, come vi ho detto, gli spazii che si misurano dal cadente, crescono in duplicata proporzione, cioè secondo i quadrati de' tempi, essendoché il tempo di un minuto primo è duodecuplo del tempo di cinque secondi, se noi multiplicheremo le cento braccia per il quadrato di 12, cioè per 144, averemo 14400, che sarà il numero delle braccia che il mobile medesimo passerà in un minuto primo d'ora; e seguitando lamedesima regola, perché un'ora è 60 minuti, multiplicando 14400, numero delle braccia passate in un minuto, per il quadrato di 60, cioè per 3600, ne verrà 51840000, numero delle braccia da passarsi in un'ora, che sono miglia 17280.
E volendo sapere lo spazio che si passerebbe in 4 ore, multiplicheremo 17280 per 16 (che è il quadrato di 4), e ce ne verranno miglia 276480: il qual numero è assai maggiore della distanza dal concavo lunare al centro della Terra, che è miglia 196000, facendo la distanza del concavo 56 semidiametri terrestri, come fa l'autor moderno, ed ilsemidiametro della Terra 3500 miglia di braccia 3000 l'uno, quali sono le nostre miglia italiane.
Adunque, signor Simplicio, quello spazio dal concavo della Luna al centro della Terra, che il vostro computista diceva non potersi passare se non in assai piú di sei giorni, vedete come, facendo il computo sopra l'esperienza e non su per le dita, si passerebbe in assai meno di 4 ore; e facendo il computo esatto, si passa in ore 3, minuti primi 22 e 4 secondi.
SAGR. Di grazia, caro Signor, non mi defraudate di questo calculo esatto, perché bisogna che sia cosa bellissima.
SALV. Tale è veramente.
Però avendo ( come ho detto ) con diligente esperienza osservato come un tal mobile passa, cadendo, l'altezza di 100 braccia in 5 secondi d'ora, diremo:
Se 100 braccia si passano in 5 secondi, braccia 588 000 000 ( che tante sono 56 semidiametri della Terra ) in quanti secondi si passeranno?
La regola per quest'operazione è che si multiplichi il terzo numero per il quadrato del secondo ; ne viene 14 700 000 000, il quale si deve dividere per il primo, cioè per 100,e la radice quadrata del quoziente, che è 12 124, è il numero cercato, cioè 12 124 minuti secondi d'ora, che sono ore 3, minuti primi 22 e 4 secondi.
SAGR. Ho veduta l'operazione, ma non intendo niente della ragione del cosí operare, né mi par tempo adesso di domandarla.
SALV. Anzi ve la voglio dire, ancorché non la ricerchiate, perché è assai facile.
Segniamo questi tre numeri con le lettere A primo, B secondo, C terzo; A, C sono i numeri de gli spazii, B è 'l numero del tempo: si cerca il quarto numero, pur del tempo.
E perchè noi sappiamo, che qual proporzione ha lo spazio A allo spazio C, tale deve avere il quadrato del tempo B al quadrato del tempo che si cerca, però, per la regola aurea, si multiplicherà il numero C per il quadrato del numero B, ed il prodotto si dividerà per il numero A, ed il quoziente sarà il quadrato del numero, che si cerca, e la sua radice quadrata sarà l'istesso numero cercato.
Or vedete come è facile da intendersi.
SAGR. Tali sono tutte le cose vere, doppo che son trovate; ma il punto sta nel saperle trovare. Io resto capacissimo, e vi ringrazio; e se altra curiosità vi resta in questa materia, vi prego a dirla, perché, s'io debbo parlar liberamente, dirò, con licenzia del signor Simplicio, che da i vostri discorsi imparo sempre qualche bella novità, ma da quelli de' suoi filosofi non so d'aver sin ora imparato cose di gran rilievo.
Prossimamente posterò un’ ulteriore descrizione della velocità , fatta Galileo.
 Alla prossima…
Alla prossima…





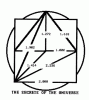

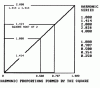

 cott Carney e Larry Pesavento.
cott Carney e Larry Pesavento.