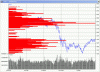
Per andare sul concreto propongo una view del Nasdaq 500 (dati EOD di Yahoo) con il Volume at Price.
Nell'uso del Volume at Price, sempre con i dati EOD, ho alcuni problemi:
1) innanzitutto l'estensione temporale del campione. Personalmente mi regolo con massimi o minimi significativi, per cui nell'esempio parto dal 31/10/2007, ma è un criterio del tutto personale. Tra l'altro estendendo troppo l'intervallo temporale credo che i dati non siano più statisticamente significativi (basta pensare per esempio all'inflazione); nell'esempio siamo a 396 giorni;
2) altra cosa le zone di minor "probabilità", nel grafico per esempio l'intervallo fra 1800 e 2150, Come le interpretate? Come valori poco "probabili" possono considerarsi due alternative:
a) l'intervallo può considerarsi come una zona difficilmente conseguibile;
b) l'intervallo, in quanto costituito da valori poco "probabili", se intaccato viene superato velocemente fino ai valori più "probabili", per esempio 2250 e 2300 (ho valutato ad occhio).
Comunque ho trovato il Volume at Price simile al Market Profile, anche se in quest'ultimo per quello che ne so si considerano solo i prezzi e non i volumi. Concettualmente simile al Market Profile mi sembra, sempre in un'ottica EOD, il Days at Price che curiosamente dà degli istogrammi simili al Volume at Price.
CraZyNasdAq e gli altri, che ne pensate?
P.S.
Per chi usa Metastock una formula per il Volume at Price è:
d:=Input("Bars to Include",1,9999,100);
n:=Input("Scaling Factor",1,99,5);
k:=Input("Plot Frame?",0,1,1);
y:=Cum(1);f:=LastValue(y);z:=f-1=y;
d:=LastValue(If(d>=f,f-1,d));a:=(f-d<y)*(y>1);
g:=a*V;b:=LastValue(Cum(g));
q:=LastValue(HighestSince(1,a=0,C));
r:=LastValue(LowestSince(1,a=0,C));
i:=(q-r)/25;u:=r+i*.5;m:=n*d/b;
x:=LastValue(Cum((C<(r+i))*g));ValueWhen(1,f-x*m<y,u);
x:=LastValue(Cum((C>=(r+i))*(C<(r+i*2))*g));ValueWhen(1,f- x*m<y,u+i);
x:=LastValue(Cum((C>=(r+i*2))*(C<(r+i*3))*g));ValueWhen(1,f- x*m<y,u+i*2);
x:=LastValue(Cum((C>=(r+i*3))*(C<(r+i*4))*g));ValueWhen(1,f- x*m<y,u+i*3);
x:=LastValue(Cum((C>=(r+i*4))*(C<(r+i*5))*g));ValueWhen(1,f- x*m<y,u+i*4);
x:=LastValue(Cum((C>=(r+i*5))*(C<(r+i*6))*g));ValueWhen(1,f- x*m<y,u+i*5);
x:=LastValue(Cum((C>=(r+i*6))*(C<(r+i*7))*g));ValueWhen(1,f- x*m<y,u+i*6);
x:=LastValue(Cum((C>=(r+i*7))*(C<(r+i*8))*g));ValueWhen(1,f- x*m<y,u+i*7);
x:=LastValue(Cum((C>=(r+i*8))*(C<(r+i*9))*g));ValueWhen(1,f- x*m<y,u+i*8);
x:=LastValue(Cum((C>=(r+i*9))*(C<(r+i*10))*g));
ValueWhen(1,f-x*m<y,u+i*9);
x:=LastValue(Cum((C>=(r+i*10))*(C<(r+i*11))*g));
ValueWhen(1,f-x*m<y,u+i*10);
x:=LastValue(Cum((C>=(r+i*11))*(C<(r+i*12))*g));
ValueWhen(1,f-x*m<y,u+i*11);
x:=LastValue(Cum((C>=(r+i*12))*(C<(r+i*13))*g));
ValueWhen(1,f-x*m<y,u+i*12);
x:=LastValue(Cum((C>=(r+i*13))*(C<(r+i*14))*g));
ValueWhen(1,f-x*m<y,u+i*13);
x:=LastValue(Cum((C>=(r+i*14))*(C<(r+i*15))*g));
ValueWhen(1,f-x*m<y,u+i*14);
x:=LastValue(Cum((C>=(r+i*15))*(C<(r+i*16))*g));
ValueWhen(1,f-x*m<y,u+i*15);
x:=LastValue(Cum((C>=(r+i*16))*(C<(r+i*17))*g));
ValueWhen(1,f-x*m<y,u+i*16);
x:=LastValue(Cum((C>=(r+i*17))*(C<(r+i*18))*g));
ValueWhen(1,f-x*m<y,u+i*17);
x:=LastValue(Cum((C>=(r+i*18))*(C<(r+i*19))*g));
ValueWhen(1,f-x*m<y,u+i*18);
x:=LastValue(Cum((C>=(r+i*19))*(C<(r+i*20))*g));
ValueWhen(1,f-x*m<y,u+i*19);
x:=LastValue(Cum((C>=(r+i*20))*(C<(r+i*21))*g));
ValueWhen(1,f-x*m<y,u+i*20);
x:=LastValue(Cum((C>=(r+i*21))*(C<(r+i*22))*g));
ValueWhen(1,f-x*m<y,u+i*21);
x:=LastValue(Cum((C>=(r+i*22))*(C<(r+i*23))*g));
ValueWhen(1,f-x*m<y,u+i*22);
x:=LastValue(Cum((C>=(r+i*23))*(C<(r+i*24))*g));
ValueWhen(1,f-x*m<y,u+i*23);
x:=LastValue(Cum((C>=(r+i*24))*(C<(r+i*25))*g));
ValueWhen(1,f-Int(x*m)=y,u+i*24);
x:=(f-d=y)*k;ValueWhen(1,x,q);ValueWhen(1,Alert(x,2),If(x,q,r));
di tale Roy Larsen.